Motion in A Straight Line - Detailed NCERT based notes Class 11 Physics Chapter 3

3. MOTION IN A STRAIGHT LINE

3.1 INTRODUCTION

Kinematics: A branch of physics that deals with the motion of an object without going into the cause of motion is known as kinematics.



Motion: The change in the position of an object with time with respect to a reference is called motion.



Rectilinear motion: The motion of an object along a straight line is called rectilinear motion.



Point object: The object whose size is much smaller than the distance it moves in a resonable duration of time are considered to be a point object.

3.2 POSITION, PATH LENGTH AND DISPLACEMENT

Reference point : An arbitrary point taken as origin serves as the reference point.



Frame of reference :The coordinate system along with a clock is called a frame of reference .

➤If one or more coordinates of an object change with time, the object is said to be in motion. Otherwise the object is said to be in rest with respect to this frame of reference. Thus, motion is a relative term.

Position :The position of an object can be specified with coordinates with reference to a conveniently chosen origin.



Path length/Distance: The total length of the path traversed by an object is called its path length.

➤Its unit is metre(m).

➤It is a scalar quantity (the quantity which has magnitude only).

Displacement ($\Delta x$): The shortest distance between initial and final positions of an object is called its displacement.

➤Its unit is metre(m).

➤It is a vector quantity (the quantity which has both magnitude and direction as well as obeys vector's laws).

NOTE : (i) Path length is greater or equal to the magnitude of the displacement between the same points.

(ii) The magnitude of the displacement for a course of motion may be zero but the corresponding path length is not zero.

(iii) Any vector quantity should have a specified direction but it is not sufficient condition for a quantity to be a vector. For example, electric current flowing in a wire has a direction but it is not a vector because it does not obey vector's law.



Uniform motion and non-uniform motion : If an object moving along a straight line covers equal distances in equal intervals of time, it is saide to be in uniform motion along a straight line. Otherwise it is called non-uniform motion.

(a) Position - time graph of an object in uniform motion

➤In equal intervals of time, equal distances are covered.

(b) Position - time graph of an object in non - uniform motion

➤In equal intervals of time, unequal distances are covered.

(c) Position - time graph of a stationary object

➤As time (t) increases, the distance(X) covered does not change.

3.3 AVERAGE VELOCITY AND AVERAGE SPEED

Average velocity :The change in position or displacement ($\Delta x$) divided by the time intervals ($\Delta t$) in which displacement occurs is called average velocity.

$\bar{v}$ = $\frac{x_2 - x_1}{t_2 - t_1}$ = $\frac{\Delta x}{\Delta t}$

Geometrically, the slope of the straight line connecting the initial position and the final position is called average velocity.



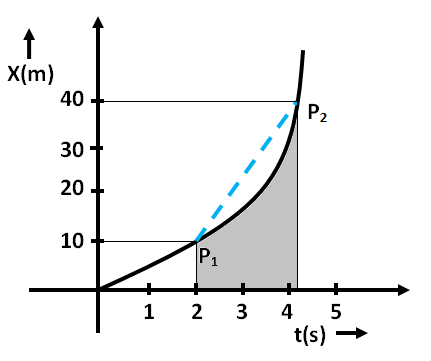
Fig. : The average velocity is the slope of line $P_1P_2$ ($P_1 $: Initial position; $P_2$ : Final position)

➤Its unit is metre per second ($ms^{-1}$).

➤It is a vector quantity.

Average speed :The total path length travelled divided by the total time interval during which the motion has taken place is called average speed.

Average speed = $\frac{total \hspace{0.1cm} path \hspace{0.1cm} length}{total \hspace{0.1cm} time \hspace{0.1cm} interval}$

➤Its unit is metre per second ($ms^{-1}$).

➤It is a scalar quantity.

NOTE : The average speed of an object is greater than or equal to the magnitude of the average velocity over a given time interval.

3.4 INSTANTANEOUS VELOCITY AND SPEED

Instantaneous velocity (velocity) :The rate of change of position with respect to time at an instant is called instantaneous velocity at that instant

or

the limit of the average velocity as the time interval $\Delta t$ becomes infinitesimally small is called instantaneous velocity.

v = $\lim \limits_{\Delta \to 0}\frac{\Delta x}{\Delta t}$ = $\frac{dx}{dt}$

Geometrically, the slope of the tangent drawn on the position - time graph at an instant is called instantaneous velocity at that instant.


Source:NCERT Book

Fig. : Velocity at t = 4s is the slope of the tangent to the x - t graph at that instant

➤Its unit is metre per second ($ms^{-1}$).

➤It is a vector quantity.

NOTE :(i) For uniform motion, velocity is the same as the average velocity at all instants.

(ii) The area under the velocity - time graph represents displacement over a given time interval.






Other Graphs

(a) Position - time graph for an object moving with positive velocity

➤As time(t) increases, the displacement (X) also increases.

Source:NCERT Book

(b) Position - time graph for an object moving with negative velocity

➤As time(t) increases, the displacement (X) decreases.

Source:NCERT Book

Instantaneous speed (speed):Instantaneous speed at a particular instant is the magnitude of velocity at that instant.

➤Its unit is metre per second ($ms^{-1}$).

➤It is a scalar quantity.

3.5 ACCELERATION

Average acceleration :The change in velocity ($\Delta v$) divided by the time intervals ($\Delta t$) is called average acceleration.

$\bar{a}$ = $\frac{v_2 - v_1}{t_2 - t_1}$ = $\frac{\Delta v}{\Delta t}$

Geometrically, the slope of the straight line connecting the initial velocity and the final velocity is called average acceleration.



Fig. : The average acceleration is the slope of line $v_1v_2$ ($v_1 $: Initial velocity; $v_2$ : Final velocity)

➤Its unit is metre per second ($ms^{-2}$).

➤It is a vector quantity.

Instantaneous acceleration (acceleration) :The rate of change of velocity with respect to time at an instant is called instantaneous acceleration at that instant

or

the limit of the average acceleration as the time interval $\Delta t$ becomes infinitesimally small is called instantaneous acceleration.

a = $\lim \limits_{\Delta \to 0}\frac{\Delta v}{\Delta t}$ = $\frac{dv}{dt}$

Geometrically, the slope of the tangent drawn on the velocity - time graph at an instant is called instantaneous acceleration at that instant.


Source:NCERT Book (Edited)



Fig. : Acceleration at t = 4s is the slope of the tangent to the v-t graph at that instant

➤Its unit is metre per second ($ms^{-2}$).

➤It is a vector quantity.

NOTE : The area under the acceleration - time graph represents average velocity over a given time interval.



Other Graphs

Source:NCERT Book

(a) Position - time graph for an object moving with positive acceleration (Graph should have concavity upward)

(b) Position - time graph for an object moving with negative acceleration (Graph should have concavity downward)

(c) Position - time graph for an object moving with zero acceleration (Graph should have a straight line)

3.6 KINEMATIC EQUATIONS FOR UNIFORMLY ACCELERATED MOTION

(i) v = $v_0$ + at

Derivation :

Say,

v : The velocity of an object at an instant.

$v_0$ : Initial velocity.

a : Acceleration.

t : The time taken.

So, by definition

a =$\frac{v -v_0}{t}$ => v - $v_0$ = at

v = $v_0$ + at

(ii) x = $v_0 t + \frac{1}{2}at^2$

Derivation :

Say,

x : The displacement of an object at an instant.

$v_0$ : Initial velocity.

a : Acceleration.

t : The time taken.

We know that area under v - t curve represents displacement.

So, according to the following graph, we have



Source:NCERT Book

x =$\frac{1}{2}(v - v_0)t + v_0t$ , where v : The velocity of an object at an instant.

But v - $v_0$ = at (from (i))

Therefore, x = $ \frac{1}{2}at^2 + v_0t$

x = $v_0 t + \frac{1}{2}at^2$

(iii) $v^2$ = $v_0 ^2 + 2ax$

Derivation : Method - 1 :

Say,

v : The velocity of an object at an instant.

$v_0$ : Initial velocity.

a : Acceleration.

x : The displacement of an object at an instant. So, we can write

x = $\bar{v}t$ , where $\bar{v}$ : The average velocity.

But, $\bar v$ = $\frac{v+v_0}{2}$ (constant acceleration only)

x = $\frac{v+v_0}{2}t$

But, t = $\frac{v - v_0}{a}$ (from (i))

x = $\frac{v+v_0}{2} \frac{v - v_0}{a}$

2ax = $v^2 - v_0^2$

$v^2 = v_0^2$ + 2ax

Derivation : Method - 2 :

We have,

x = $v_0 t + \frac{1}{2}at^2$ (from (ii))

But, t = $\frac{v - v_0}{a}$ (from (i))

x = $v_0 \frac{v - v_0}{a} + \frac{1}{2}a(\frac{v - v_0}{a})^2$

x = $ \frac{ (v - v_0)}{2a} (2v_0 + v - v_0)$

x = $ \frac{ (v - v_0)}{2a} ( v +v_0)$

2ax = $v^2 - v_0^2$

$v^2 = v_0^2$ + 2ax

NOTE : These three equations were obtained by assuming that at t=0, the position of the particle, x is 0. If the position coordinate at t=0 as non-zero, say $x_0$, then x is replaced with ($x - x_0$)

(i) $v = v_0 + at $

(ii) x = $x_0 + v_0 t + \frac{1}{2}at^2$

(iii) $v^2$ = $v_0 ^2 + 2a(x - x_0)$



Deriving these three equation using method of calculus



(i) v = $v_0$ + at

Derivation :

By definition

a = $\frac{dv}{dt}$ => dv = a dt

Integrating both sides

$\int_{v_0}^v{dv} = \int_{0}^t{adt}$

But, a is constant

$\int_{v_0}^v{dv} = a \int_{0}^t{dt}$

v - $v_0$ = at

v = $v_0$ + at

(ii) x = $v_0 t + \frac{1}{2}at^2$

Derivation :

By definition

v = $\frac{dx}{dt}$ => dx = v dt

Integrating both sides

$\int_{x_0}^x{dx} = \int_{0}^t{vdt}$

but v = $v_0 + at $

$\int_{x_0}^x{dx} = \int_{0}^t{(v_0 + at)dt}$

x - $x_0$ = $v_0 t + \frac{1}{2}at^2$

x = $x_0 + v_0 t + \frac{1}{2}at^2$

(iii) $v^2$ = $v_0 ^2 + 2ax$

Derivation :

We can write

a = $\frac{dv}{dt} = \frac{dv}{dx}\frac{dx}{dt} = v\frac{dv}{dx}$

vdv = a dx

Integrating both sides

$\int_{v_0}^v{vdv} = \int_{x}^{x_0}{adx}$

$\frac{v^2 - v_0^2}{2} = a (x - x_0)$

$v^2$ = $v_0 ^2 + 2a(x - x_0)$

NOTE :The advantage of the method of calculus is that it can be used for motion with non-uniform acceleration also.

➤ Some Collected Important Facts :

♞ Free fall : A body is said to be in free fall if it moves under only force of gravity .

♞ Galileo's law of odd numbers : The distances trversed, during equal intervals of time, by a body falling from rest, stand to one another in the same ratio as the odd numbers beginning with unity [namely, 1:3:5:7...].

♞ Stopping distance of vehicles : When brakes are applied to a moving vehicle, the distance it travels before stopping is called stopping distance.

♞ Reaction time : The time taken to observe, think and act by a person is called his reaction time.

3.6 RELATIVE VELOCITY

Relative velocity : The relative velocity of an object A with respect to an object B is defined as the velocity of the object A minus the velocity of the object B.

Say,

$V_A$ = Velocity of an object A

$V_B$ = Velocity of an object B

$V_{AB}$ = The relative velocity of the object A with respect to the object B

$V_{AB}$ = $V_A - V_B$

Graphs

(a) Position - time graphs of two objects with equal velocities




Source:NCERT Book

(b) Position - time graphs of two objects with unequal velocities, showing the time of meeting
Source:NCERT Book

(c) Position - time graphs of two objects with velocities in opposite directions, showing the time of meeting
Source:NCERT Book